新课标卷最能体现这些转变,它更注重基础性,强调综合性、应用性和创新性,“让套路限行、让刷题失效”。所以出题时也体现出反套路的特点,
下面是一些典型题:
例1(2021级资阳一诊16题)
若函数$f(x)=e^x+cosx+(a-1)x$存在最小值,则$a$的取值范围是________.
解法1:
答案:$(-\infty,1)$
解答:
注意到, 当 $ a=1 $ 时, $ f(x)=\mathrm{e}^{x}+\cos x $, 由于 $ \mathrm{e}^{x}>0,-1 \leqslant \cos x \leqslant 1 $, 显然 $ f(x) \rightarrow-1 $,没有最小值;
当 $ a>1 $ 时, $ \mathrm{e}^{x}+\cos x>-1 $ 且无限接近 $ -1, y=(a-1) x $ 为增函数,
则 $ x \rightarrow-\infty, \mathrm{e}^{x} +\cos x+(a-1) x \rightarrow-\infty, x \rightarrow+\infty, \mathrm{e}^{x}+\cos x+(a-1) x \rightarrow+\infty $, 此时没有最小值;
当 $ a<1 $ 时, $ y =(a-1) x $ 为减函数, 则 $ x \rightarrow-\infty, \mathrm{e}^{x}+\cos x+(a-1) x \rightarrow+\infty, x \rightarrow+\infty $,
由于 $ y=\mathrm{e}^{x} $ 增长变化速度远大于 $ y=(a-1) x $ 减少速度, 此时 $ \mathrm{e}^{x}+\cos x+(a-1) x \rightarrow+\infty $,
也可以结合大致图象特征判断, $ f(x)=\mathrm{e}^{x}+\cos x+(a-1) x $ 存在最小值.
下面是三种情况对应的图象
1当$a>1$时
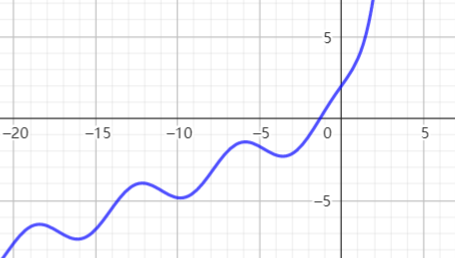
当$a=1$时
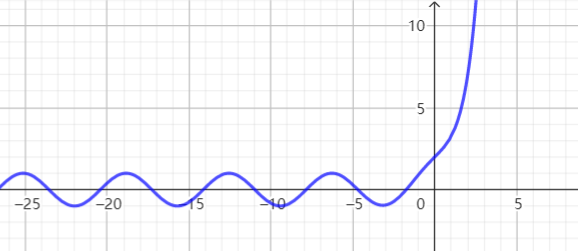
当$a<1$时





